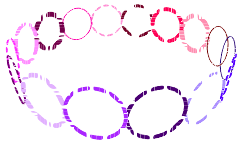Examples > Primitives

Circles.

Let's create an array of circles with centers lying on the circle and normals directed to the centre of this circle.

Let the variation interval of the angle moving along the circle be from 0 to Pi.

Let the variation angle step be equal to 0.4 radians, the circle radius with the centers be equal to 5, and the radii of the circles themselves be the same and equal to 1.

Let's calculate the color, thickness and styles of the circles on the following formulas:

circle color number from palette = residue of division integer part (10*angle) by 200+50;

circle thickness = residue of division integer part (10*angle) by 5;

circle style number = residue of division integer part (10*angle) by 5;

So, the function of creating the necessary line segments array will look like this:

for (double i=0.0;i<2.0*3.14159265;i+=0.4)

{

SG_POINT crCen = {5.0*cos(i),5.0*sin(i),0.0};

SG_VECTOR crNor;

crNor.x = crCen.x - 0.0;

crNor.y = crCen.y - 0.0;

crNor.z = 0.0;

sgSpaceMath::NormalVector(crNor);

SG_CIRCLE crGeo;

crGeo.FromCenterRadiusNormal(crCen, 1, crNor);

sgCCircle* cr = sgCreateCircle(crGeo);

sgGetScene()->AttachObject(cr);

cr->SetAttribute(SG_OA_COLOR,((int)(10*i))%200+50);

cr->SetAttribute(SG_OA_LINE_THICKNESS, ((int)(10*i))%5);

cr->SetAttribute(SG_OA_LINE_TYPE, ((int)(10*i))%5);

}